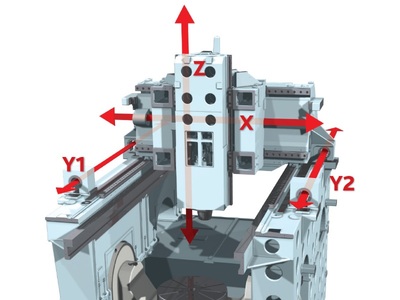
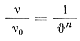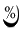Определение скоростей и давлений в сечении ламинарного потока

Определение скоростей и давлений в сечении ламинарного потока по эксперементальным зависимостям вязкости от температуры

Построим закон распределения скоростей в идеальном случае (v = const).

Рассмотренное ранее уравнение (17) превратится в

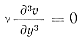
Так как v ≠ 0, то д³υ/ду³ = 0 или после интегрирования

υ = C₁ + С₂у + C₃у³.

После нахождения постоянных C₁, C₂ и С₃ из граничных условий, что при у = 0, υ = υ_max и у = ±Н/2, υ = 0, и подстановки их получим параболический закон

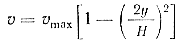
После замены υ_max через υ_ср, найденное из секундного расхода, имеем

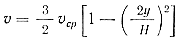                       (27)

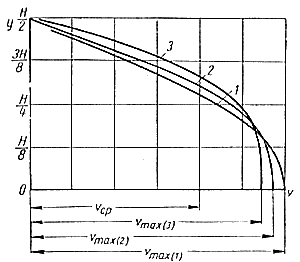Графическое изображение закона (27) дано на рис. 38 (кривая 1). Реальные законы распределения скоростей (кривые 2 и 3 на рис. 38) значительно отличаются от параболического и тем больше, чем больше безразмерная величина m в уравнении для определения зависимости вязкости от температуры (уравнение 21). Рис. 38. Изменение скоростей по сечению ламинарного потока расплавленного  металла

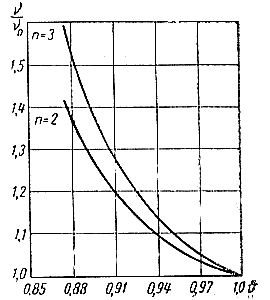Для алюминиевых сплавов, заливаемых в кашеобразном состоянии, наиболее подходящей является гиперболическая экспериментальная зависимость (рис. 39) в которой показатель степени n меняется от 2 до 3. Соответственно в уравнении (21) безразмерная величина С = 1, а величина m меняется от β до 1,5 β. На рис. 39 кривая 2 построена при условии m = β, а кривая 3 при m = 1,5 β. Рис. 39.Экспериментальные зависимости вязкости от температуры в виде — = v/v0=φ(знак)

Значения 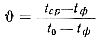на рис. 39 получены при условии, что t_ф=200°, t₀ = 600°, а t_ср меняется от 600 до 550° С.

Если m = β = 2, закон распределения скоростей (уравнение 24) принимает вид

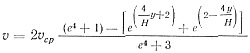
откуда при у = 0 определяем υ_max:

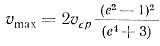             (28)

Закон изменения давления на пути l при m = β = 2 после преобразования формулы (26) примет вид

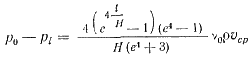             (29)

После подстановки числовых значений для алюминиевых сплавов v₀ =2,23·10^-6 м2/сек (для кашеобразного сплава) и ρ = 2700 кг/м3 получим

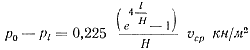
где H и / в мм, а υ_ср в м/сек.

В идеальном случае, если не учитывается изменение вязкости, закон изменения давления определится после подстановки значения υ из выражения (27) в уравнение

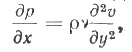
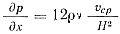
откуда после интегрирования в пределах изменения давления от р₀ до p₁ и x от 0 до l получим

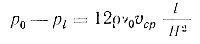
или для алюминиевых сплавов

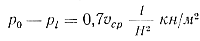
Следовательно, падение давления зависит главным образом от толщины отливки. Чем тоньше отливка, тем больше падение давления.

Например, для отливки из сплава АЛ2 длиной l = 400 мм и толщиной H = 8 мм при средней скорости потока υ_ср = 5 м/сек падение давления (потеря гидродинамического напора)

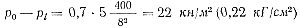
Для тех же условий при толщине отливки H = 2 мм

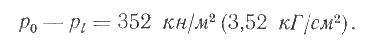
При ламинарном движении нет захвата воздуха в полости формы — воздух направленно вытесняется потоком металла к вентиляционным каналам. Однако воздушные пузырьки могут попасть в расплавленный металл в камере прессования или при разрыве потока в расширяющейся литниковой системе.

Кроме этого, в потоке возможно образование газовых включений, выделяющихся из твердых растворов во время кристаллизации. На возможность газовыделения при вакуумировании указывали Л. А. Гаспарян и P. M. Калиш. Данные исследований Р. А. Короткова доказывают наличие газовыделения и при невакуумированном литье под давлением.

При ламинарном движении возможен вынос пузырьков газа в зону максимальных скоростей, теоретически обоснованный для литья под давлением П. П. Москвиным.

Величина подъемной силы Р_под прямо пропорциональна квадрату скорости потока в максимальной зоне υ_max:

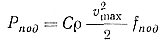
где С — безразмерный коэффициент, зависящий от геометрической формы вытесняемого тела и числа Рейнольдса, для шара при Re < 2000 равен ⅓;  ƒ_под — площадь поперечного сечения  пузырька  в  плоскости подъема, для шара ƒ_под площадь поперечного сечения пузырька в плоскости подёъма, для шара ƒ_под = πd2_под / 4.

Величина подъемной силы часто оказывается недостаточной для преодоления сопротивления затвердевающего металла. Если максимальная скорость υ_max, которая в идеальном случае в 1,5 раза больше средней скорости потока υ_max = 1,5 υ_ср, составляет 7,5 м/сек, то для пузырька газа диаметром 1 мм подъемная сила в алюминиевом сплаве (ρ = 2700 кг/м3).

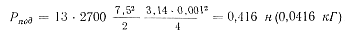
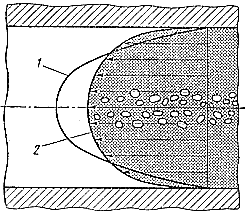В результате изменения вязкости расплавленного металла зона максимальных скоростей увеличивается и вынос пузырьков газа по центру потока еще более затрудняется (рис. 40). Следовательно, даже при ламинарном заполнении возможно образо вание газовой пористости, для полной ликвидации которой необходимо тщательно   рафинировать сплав и не допускать нарушения сплошности  потока в литниковой системе. Рис. 40. Образование газовой пористости в зоне максимальных скоростей: 1 — параболический закон изменения скорости; 2 — изменение скорости а потоке с переменной низкостью