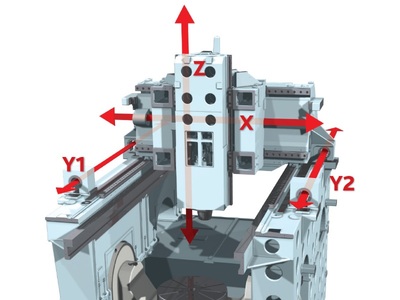
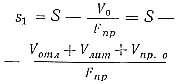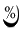В процессе заполнения литниковой системы и формы
В процессе заполнения литниковой системы и формы расплавленным металлом возникают дополнительные гидродинамические сопротивления, снижающие скорость движения прессующего поршня.
Величина гидродинамических сопротивлений в литниковой системе различна для машин с горизонтальной, вертикальной или горячей камерой прессования.
Сопротивление движению металла в полости формы зависит от конфигурации отливки. Чем сложнее отливка, тоньше ее стенки, больше в ней поворотов и резких переходов, тем больше величина гидродинамического сопротивления формы.
Потери давления в результате трения о стенки литниковых каналов и формы пропорциональны вязкости расплавленного металла. Например, при ламинарном течении коэффициент трения по длине
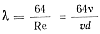
Следовательно, при понижении температуры металла (при заливке кашеобразным сплавом) гидродинамические сопротивления возрастают в несколько раз.
Как указывают Б. Б. Гуляев и А. А. Гетьман, действительные коэффициенты расхода в литниковых системах зависят также от времени течения металла и толщины намерзающей корочки.
В процессе заполнения в форме возникает противодавление воздуха. При нормальном технологическом режиме работы противодавление воздуха невелико и его можно не учитывать при расчете скорости прессования. Однако при недостаточной площади вентиляционных каналов или засорении их противодавление достигает значительной величины.
 |
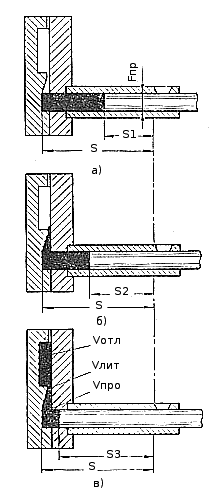Рассмотрим три стадии движения прессующего поршня в процессе заполнения для машин с горизонтальной камерой прессования (рис. 64). В теоретических исследованиях Б. Закса путь поршня разбивается на шесть участков, однако первые три участка, соответствующие разгону поршня и созданию установившейся скорости движения, не представляют интереса при разработке технологического процесса. 1. Пepвая стадия (рис. 64, а) заканчивается одновременно с периодом установившегося движения прессующего поршня. За начало первой стадии условно принимаем начало второй ступени прессования после перекрытия заливочного окна. В этом случае путь поршня
где S — полный ход поршня от начала перекрытия заливочного окна; V0 — объем заливаемого металла, складывающийся из объема отливки Vотл объема литниковых каналов Vлит и объема прессостатка Vпр.о. Скорость прессования на первой стадии равномерна и определяется по формуле (44). Рис. 64. Движение поршня в камере прессования |
2. Втоpая стадия (рис. 64, б) заканчивается после заполнения литниковой системы. К концу второй стадии поршень пройдет путь
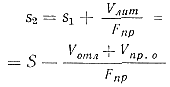
3. Третья стадия (рис. 64, в) заполнения формы. Путь поршня соответствует процессу заполнения формы. Путь поршня
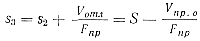
Формулы Б. Закса для определения скорости прессования на различных стадиях движения поршня чрезвычайно громоздки и выведены из условий удаления воздуха с максимальной скоростью только в окончательный период заполнения. Это положение, как отмечает X. Бартон, не имеет ничего общего с действительным процессом литья под давлением, при котором следует создавать условия для выхода воздуха до начала поступления металла в форму.
Расчеты по формулам Б. Закса, проведенные Г. Либи, значительно превышают реальные значения скоростей прессования.
Скорость прессования на второй и третьей стадиях можно определить из уравнения равновесия сил, действующих на поршень, при этом считать его движение в каждый момент определения скорости установившимся.
На основе принципа Даламбера составим уравнение сил при движении поршня в камере прессования:
Pпр = Pг.с + Pин, (46)
где Рпр — усилие прессования, развиваемое прессовым поршнем при его движении; Pг.с — сила суммарных гидродинамических сопротивлений движению металла в литниковой системе и форме; Pин — иyерционная сила подвижных частей прессующего механизма.
Усилие прессования создается давлением рабочей жидкости в полости цилиндра рпр, действующим на площадь прессового поршня Fц:
Рпр = РпрFц
Давление жидкости в полости цилиндра определяется из уравнения Бернулли для аккумулятора и цилиндра прессования:
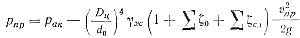
Соответственно усилие прессования
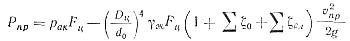(47)
Сила суммарных гидродинамических сопротивлений определяется по методу, использованному А. И. Вейником при аналитическом исследовании процесса движения поршня:
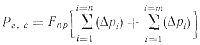
где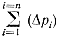 
— суммарное
противодавление, возникающее в литниковой системе; 
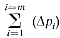— суммарное противодавление в форме. Потери
давления на i-м участке движения расплавленного металла определяются
выражением
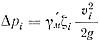
где γ'м — удельный вес жидкого металла; ζi — коэффициент сопротивления на i-м участке; υi — скорость движения металла в i-м сечении.
Так как
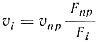
то можно записать
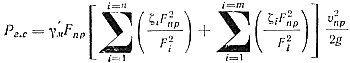(48)
Сила инерции Рин входящая в уравнение (46), находится из закона Ньютона:
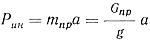(49)
где Gпр — вес подвижных частей прессующего механизма в н.
Ускорение а, согласно определению А. И. Вейника, можно приближенно представить в виде
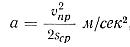
где υпр — средняя скорость прессования на участке заполнения в м/сек; sср — средний путь поршня на второй и третьей стадиях движения в м.
Согласно обозначениям на рис. 64
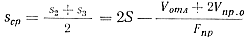
После подстановки значения ускорения а в уравнение (49) получим зависимость инерционной силы от скорости:
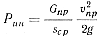(50)
Перепишем уравнение сил (46) с заменой его слагаемых через выражения (48), (49) и (50) и вынесем за скобки величину υ2пр/2g.
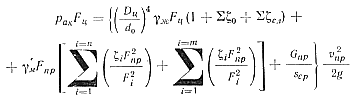
Из этого выражения находим формулу для расчета скорости прессования:
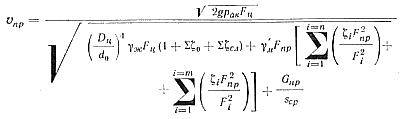(51)
В формуле (53) произведение ракFц = Рпр представляет номинальное усилие прессования для данной машины.
Величина гидродинамических сопротивлений в литниковой системе и форме, определяемая вторым слагаемым в знаменателе формулы (53), прямо пропорциональна удельному весу сплава γ'м. Следовательно, при заполнении формы цинковыми и медными сплавами скорость прессования будет уменьшаться на большую величину по сравнению с заливкой алюминиевыми и магниевыми сплавами. Это необходимо учитывать при выборе мощности машины.
Если не учитывать сопротивление в литниковой системе и форме и пренебречь весом подвижных частей Gпр = 0, то формула (51) превратится в формулу (44) для определения скорости холостого хода прессующего поршня. При использовании мощных машин с диаметром цилиндра прессования Dц > 200 мм скорость прессования почти не зависит от гидравлических сопротивлений, так как второй член подкоренного выражения в формуле (51) становится очень малым по сравнению с первым.
Для определения по формуле (51) скорости прессования необходимо задаться определенной конструкцией и размерами литниковой системы и формы, с тем чтобы вычислить конкретные значения гидродинамических сопротивлений.
