Общие уравнения работы однофазных трансформаторов могут быть получены из упрощенных эквивалентной схемы замещения и векторного треугольника (рис. 18.5).
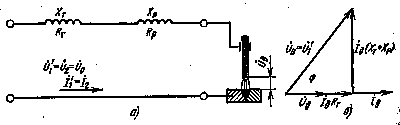
Рис. 18.5. Однофазный трансформатор: а — упрощенная схема замещения; б — векторная диаграмма
Зависимость напряжения дуги от тока в векторной форме можно записать
Uд = U0 — I2 [(Xт + Хр) + ( Rт + Rр)],
где Хт = Х'1 + Х2 — суммарное индуктивное сопротивление трансформатора; Хр — индуктивное сопротивление реактивной катушки; Rт = R'1 + R2 — суммарное активное сопротивление трансформатора; Rp — активное сопротивление реактивной катушки; Х'1, R'1 — приведенные индуктивное и активное сопротивления первичной обмотки трансформатора.
Это уравнение внешней вольт-амперной характеристики однофазного трансформатора для дуговой сварки.
Напряжение дуги согласно векторной диаграмме
Uд = √U20 — I2д (Хт + Хр)2 — Iд (Rт + Rp)
Пренебрегая малыми величинами Rт и Rp, получим
Uд≈√U20 — I2д (Хт + Хр)2, (18.1)
откуда
Iд≈√U20 — U2д (Хт + Хр) (18.2)
При коротком замыкании (Uд = 0; тогда ток короткого замыкания
Iк.з = U0/(Хт + Хр). (18.3)
Из приведенных уравнений следует, что необходимая для устойчивого горения дуги индуктивность может быть получена либо в самом трансформаторе (при Хр≈0), либо включением в цепь дуги реактивной катушки (при Хт≈0). Наличие индуктивности обеспечивает получение крутопадающей внешней характеристики источника и возможность его настройки на заданный режим работы.
В зависимости от способа создания в цепи дуги индуктивного сопротивления трансформаторы разделяют на две группы. Первую группу составляют трансформаторы с увеличенным магнитным рассеянием (Хт≈0) без реактивной катушки (Хр = 0), вторую — с нормальным магнитным рассеянием (Хт≈0) в сочетании с реактивной катушкой (Хр≠0).