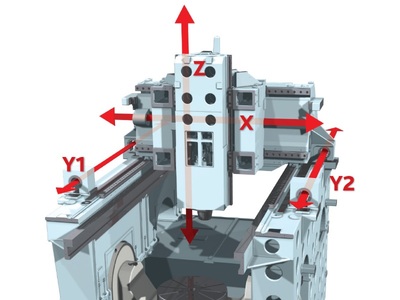
Одним из основных методов исследования температурного поля является математический анализ теплового потока от отливки к форме, дающий возможность оценить физические явления процесса теплопередачи.
Для дальнейшего рассмотрения тепловых процессов при литье под давлением необходимо ознакомиться с основами общей теории теплопередачи и теории подобия, которые в наиболее простой и в то же время строгой форме изложены в монографии А. И. Вейника «Тепловые основы теории литья».
В общем виде процесс распространения тепла определяется дифференциальным уравнением Фурье — Кирхгофа:
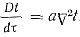 (63)
(63)
где Dt/dτ - полная (субстанциальная) производная, отражающая изменение температуры как во времени, так и в пространстве,
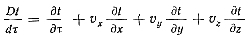
а — коэффициент температуронроводимости; ∇2t — оператор Лапласа;
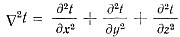
После прекращения движения расплавленного металла в момент окончательного заполнения формы левая часть уравнения (63) зависит только от времени Dt/dτ= ∂t/ ∂τ и уравнение (63) принимает вид
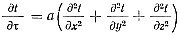 (64)
(64)
Последнее уравнение называется дифференциальным уравнением теплопроводности Фурье.
Для одномерного поля, в котором температура изменяется только вдоль одной оси (плоская отливка, тонкостенная коробчатая или цилиндрическая отливка), уравнение теплопроводности еще больше упрощается:
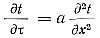 (65)
(65)
Уравнения (63), (64) и (65) представляют собой только общую связь между изменениями температур во времени и пространстве.
Чтобы получить из множества возможных решений конкретное решение, необходимо определить условия однозначности.
Для заданного тела (тела определенной геометрической формы с определенными физическими свойствами; кроме того, для упрощения решений в дальнейшем физические свойства λ, с, ρ будем считать постоянными) условия однозначности сводятся к заданию начальных и граничных условий.
Начальные (временные) условия характеризуют состояние системы в исходный момент времени. Например, при рассмотрении заполнения формы в начальный момент (при τ = 0) температура расплавленного металла равна температуре заливки минус потери в литниковой системе (t = tзал — Δtл.c).
Граничные условия характеризуют тепловое взаимодействие между отливкой и формой. Теплообмен на поверхности тела описывается уравнением закона Ныотона:
q = α(t-tф), (66)
где t — температура расплавленного или затвердевшего металла отливки; tф — температура поверхности формы; α — коэффициент теплоотдачи.
Полное количество теплоты, передающееся через поверхность dF за элементарный отрезок времени dτ, определяется выражением:
d2Q = α(t — tф)dFdτ. (67)
Коэффициент теплоотдачи а в выражениях (66) и (67) является постоянной величиной только при малых значениях разности температур (t— tф). В условиях литья под давлением коэффициент а зависит от времени, конфигурации отливки, величины перепада температур между отливкой и формой.
Точное решение задачи затвердевания возможно лишь в простейших случаях. Примером такого решения является решение Стефана для плиты. Однако его использование в расчетах затрудняется определением корней трансцендентных уравнений.
Более простой способ приближенного решения дифференциального уравнения теплопроводности предложен И. Д. Семикиным и 3. M. Гольдфарбом. Воспользуемся этим решением для определения времени затвердевания плоской отливки в стальной массивной пресс-форме, считая, что форма заполняется почти мгновенно, без существенного охлаждения расплавленного металла. Такое допущение возможно при заполнении массивной отливки ламинарным или квазиламинарным (при переходе от ламинарного к турбулентному) потоком через толстый питатель.
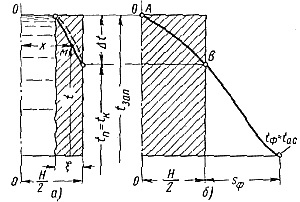 |
Процесс затвердевания сопровождается выделением скрытой теплоты затвердевания и постоянным нарастанием толщины затвердевшего слоя ξ (рис. 80,a). Рис. 80. Схема затпердевания отливки: а — нарастание затвердевшего слоя; б — полное затверлевание отливки и прогрев формы толщиной sф |
Разберем наиболее простой случай охлаждения при постоянном тепловом потоке через затвердевшую корку.
Дифференциальное уравнение теплопроводности одномерного поля (65) можно записать в следующем виде:
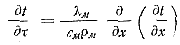 (68)
(68)
где t — температура в любой точке M на расстоянии x от центральной оси отливки OO; λм, см и ρм — коэффициент теплопроводности, удельная теплоемкость и плотность металла отливки.
Основные допущения при определении температурного поля:
- а) независимое рассмотрение температурных полей отливки и формы.
- б) прямолинейное распределение температур по сечению затвердевшего слоя,
- в) влияние выделения скрытой теплоты затвердевания учитывается косвенным увеличением теплоемкости затвердевшего слоя отливки.
- г) отсутствие зазора между отливкой и формой, а также отсутствие слоя смазки.
При отсутствии смазки в условиях литья под давлением зазор начинает образовываться после снятия давления на металл (после полного затвердевания литниковой системы).
Начальные условия для температуры означают, что температура на границе раздела жидкого и затвердевшего металла постоянна и равна температуре затвердевания t = tзат = const.
Температуру поверхности отливки и формы при отсутствии зазора можно принять равной температуре контакта tп = tк. В момент соприкосновения жидкого металла с формой происходит мгновенный разогрев поверхности и некоторое охлаждение металла, причем температура заливаемого металла tзал и стенок формы tф стремится к одномузиаченню, определяемому формулой
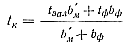
где b'м=√λ'мс'мρ'м — коэффициент аккумуляции тепла в жидком металле в вт·сек ½ /м2°С;
bф = √λфcфρф — коэффициент аккумуляции материала формы.
Принимаем следующие граничные условия:
- а) тепловой поток на охлаждаемой поверхности постоянен, qп = const;
- б) тепловой поток на границе раздела жидкого и затвердевшего металла равен нулю, т. е. при x = H/2-ξ, q = 0.
Скорость охлаждения по сечению затвердевшего слоя толщиной ξ принята постоянной
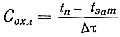
где Δτ—время затвердевания слоя. Скорость охлаждения для элементарного отрезка времени ∂τ.

С другой стороны, скорость охлаждения можно представить, как уменьшение теплового потока:
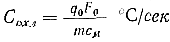
где q0 — удельный тепловой поток на поверхности слоя в вт/м2; F0 — поверхность охлаждения в м2; m — масса охлаждаемого слоя в кг; см — удельная теплоемкость металла отливки в дж/кг°С.
Отношение поверхности охлаждения к весу охлаждаемого слоя заменим через толщину слоя ξ. Так как ξ=Vм/F0 , где Vм — объем затвердевшего слоя, равный Vм = m/ρм, то ζ = m/ρмF0 , откуда F0/m=1/ξρм. Подставляя это значение отношения F0/m в выражение скорости охлаждения, получим
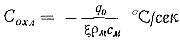
В случае полного затвердевания отливки значение скорости охлаждения при ξ=Н/2 подставим в дифференциальное уравнение (68) после интегрирования с учетом граничных условий и получим следующее выражение для температурного поля отливки:
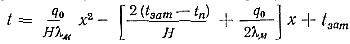
Если x = 0 (рис. 80, б), то температура в центре отливки равна температуре затвердевания t = tзат. При x=Н/2 температура стремится к температуре контакта на поверхности отливки t→tп = tк.
Изменение температуры по сечению отливки представлено на рис. 80, б кривой AB. Необходимо учитывать, что кривая AB построена для полностью затвердевшей отливки. В затвердевшем слое толщиной ξ принят прямолинейный закон изменения температуры. Перейдем к определению продолжительности затвердевания при допущении постоянства теплового потока.
Формула для определения перепада температур по толщине охлаждаемого слоя имеет вид:
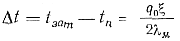 (70)
(70)
Средняя температура по толщине слоя tср с учетом неравномерности распределения температур
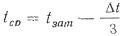 (71)
(71)
Зависимость между толщиной охлаждаемого слоя и временем может быть получена из уравнения теплового баланса:
q0τ = ξρмсм(tзат - tср)
После подстановки вместо tср ее значения из выражения (71), в котором заменяем перепад температур Δt его значением из формулы (70), определим время затвердевания
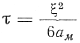
Полное время затвердевания отливки τзат будет найдено при ξ=Н/2
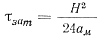 (72)
(72)
При выводе данной формулы тепловой поток считается неизменным. В реальных условиях он изменяется за счет выделения теплоты затвердевания.
Для учета влияния скрытой теплоты затвердевания заменим коэффициент 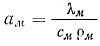 условным коэффициентом
температуропроводимости:
условным коэффициентом
температуропроводимости:
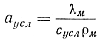
где
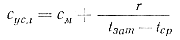
r — скрытая теплота затвердевания в дж/н.
Подставляя значение аусл в формулу (72) и заменяя tcp ее значением из выражения (71), получим
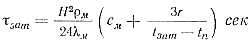 (73)
(73)
Принимая в формуле (73) разность tзат — tп равной для цинковых сплавов 250°С, для алюминиевых и магниевых 450°С и для медных 750°С, получим расчетные формулы определения τзат в сек для различных сплавов:
| цинковых | τзат= 0,0052Н2 | } (74) |
| алюминиевых | τзат = 0,0014Н2 | |
| магниевых | τзат = 0,0022Н2 | |
| медных | τзат =0,0026Н2 |
где H — толщина отливки в мм.
На рис. 81 представлены графические зависимости времени затвердевания отливок толщиной от 2 до 10 мм для различных сплавов, из которых видно, что время затвердевания отливок из цинковых сплавов (4) намного нммг превышает время затвердевания отливок из алюминиевых (1), магниевых (2) и медных (3) сплавов. Этим объясняется высокая чистота поверхности и малая пористость отливок из цинковых сплавов.
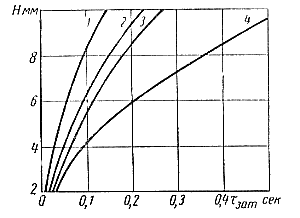 |
Значения продолжительности затвердевания, подсчитанные по аналитическим формулам (74), отличаются от действительных значений этих величин при литье под давлением на 15—30%. Рис. 81. Изменение времени затвердевания в зависимости от толщины стенки отливок для различных сплавов |