Анализ тепловых условий формирования отливки проводится на базе совместного изучения процесса распространения тепла в отливке и форме. Наиболее правильное представление о процессе распространения тепла можно получить с помощью как аналитических, так и экспериментальных методов исследования температурного поля системы «отливка — форма».
Одним из основных методов исследования температурного поля является математический анализ теплового потока от отливки к форме, дающий возможность оценить физические явления процесса теплопередачи.
Однако ввиду чрезвычайной сложности явления получить общее аналитическое решение задачи о температурном поле рассматриваемой системы средствами современной математики невозможно. Поэтому для осуществления конкретных решений используется метод теории подобия.
Критериальные уравнения теории подобия
Результаты экспериментов, применяемые только к конкретному изучаемому явлению, не могут распространяться на другие процессы. В то же время аналитические решения не позволяют перейти от класса явлений, характеризуемых дифференциальным уравнением теплопроводности, к единичному явлению.
Для объединения аналитических решений и экспериментальных исследований используется теория подобия, которая представляет собой учение о методах научного обобщения данных единичного опыта.
Основная теорема теории подобия установлена M. В. Кирпичевым и А. А. Гухманом.
Два или несколько явлений подобны, если они описываются одной и той же системой дифференциальных уравнений и имеют подобные условия однозначности.
Процессы теплопередачи в общем виде описываются системой дифференциальных уравнений, в которую входят уравнения: распространения тепла Фурье — Кирхгофа (63), движения расплавленного металла (13) и неразрывности (14).
Подобие условий однозначности обеспечивается равенством критериев подобия, представляющих собой безразмерные комплексы физических и геометрических свойств изучаемой системы.
Критерии подобия, составленные из величин, которые входят в условия однозначности называются определяющими критериями. Равенство определяющих критериев влечет за собой равенство всех остальных критериев, в состав которых входят величины, не содержащиеся в условиях однозначности.
Результаты экспериментов представляются в виде зависимостей между критериями, причем определяющие критерии являются аргументами, а неопределяющие — функциями. Такие зависимости называются критериальными уравнениями. Критериальные уравнения дают возможность определить величину коэффициента теплоотдачи а на границе отливки и формы при различных условиях литья под давлением.
Определяющие критерии при рассмотрении тепловых условий в процессе заполнения формы имеют вид
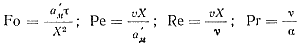
где Fo — критерий Фурье; Ре — критерий Пекле; Re — критерий Рейнольдса; Pr — критерий Прандтля; а'м — коэффициент температуропроводимости жидкого металла; υ — скорость движения потока; v — вязкость расплава; τ - время заполнения; X — определяющий размер отливки.
Неопределяющим критерием является критерий Нуссельта, характеризующий интенсивность теплообмена на поверхности жидкого металла:
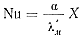
где α—коэффициент теплоотдачи соприкосновением; λ'м — коэффициент теплопроводности расплава.
Критериальное уравнение составляется в виде степенной зависимости между критериями:
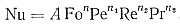(75)
Например, для стационарного (Fo = 0) турбулентного движения расплавленного металла можно использовать уравнение
Nu =0,023Re0,8Pr0,4.
Рассмотрим пример расчета теплообмена на поверхности отливки и формы с использованием критериального уравнения (75) для вычисления температуры разогрева поверхности.
В процессе заполнения интенсивность конвективного переноса тепла зависит от скорости течения металла. Чем больше скорость, тем интенсивнее теплообмен между жидким металлом и стенкой формы. Температура tф каждого участка поверхности может быть вычислена по формуле нагрева полуограниченного тела при конвективном теплообмене:
tф=tф.нач + Kt(t'м — tф.нач) (76)
где tф.нач — начальная температура формы в °С; t'м —температура жидкого металла в °С; Kt = φ(z) —коэффициент, характеризующий степень приращения температуры формы во время заполнения,
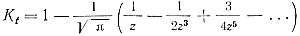
где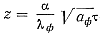 
Здесь α — коэффициент теплоотдачи конвекцией в вт/м2°С; λф — коэффициент теплопроводности формы в вт/м °С; аф — коэффициент температуропроводимости формы в м2/сек; τ — продолжительность течения жидкого металла через рассматриваемый участок в сек.
Для определения коэффициента теплоотдачи в условиях литья под давлением можно использовать приближенное критериальное уравнение, выведенное для пластины, омываемой жидким металлом,
Nu = 0,38Pe0,65.
Подставляя значения Nu =αl/λ'м и Ре = υl/a'м, найдем выражение для α
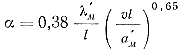
Безразмерная величина z определится выражением
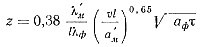
или для алюминиевых сплавов
z = 6,35υ0,65τ0,5,
если скорость течения жидкого металла υ в м/сек.
На рис. 87 дана номограмма, построенная Чжу-Сэнь-Юанем для алюминиевых сплавов, по которой можно определить величину z и коэффициент Kt в зависимости от скорости потока и времени (τ) движения его по поверхности рассматриваемого участка формы.
Определим температуру разогрева поверхности формы tф при заполнении алюминиевым сплавом (t'м = 600°С), со скоростью υ = 40 м/сек, если форма предварительно нагрета до tф.нач = 200°С и время движения потока по поверхности τ = 0,1 сек.
По номограмме (см. рис. 87) определяем величины z = 25 и Kt = 0,97. Подставив значение Kt и остальные цифровые значе-нияв формулу (76), получим tф = 200 + 0,97(600 — 200) = 588°С.
 |
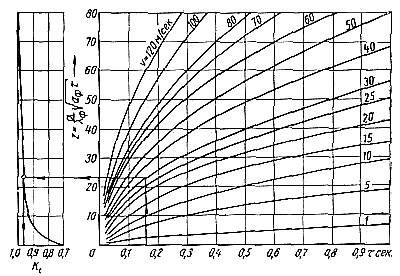Рис. 87. Номограмма для определения коэффициента Kt в зависимости от времени и скорости течения жидкого металла по поверхности формы |
Следовательно, в течение 0,1 сек поверхность формы нагревается почти до температуры заливаемого металла. Аналогичные результаты были зафиксированы в экспериментах E. Микеля (см. рис. 83).
Критериальное уравнение температурного поля затвердевшей отливки или формы имеет вид
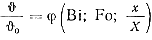(77)
где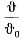 
— безразмерное
отношение искомой температуры t к начальной t0, в котором температура
отсчитывается от температуры окружающей среды tс как от нуля,
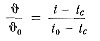
Bi=α/λ H — критерий Био, который отличается от критерия Nu суммарным коэффициентом теплоотдачи а и коэффициентом теплопроводности твердого тела λ. Критерий Bi является основной характеристикой интенсивности теплообмена на поверхности отливки.
Экспериментальные замеры и расчеты температурного поля при литье под давлением показывают, что температура отливки в процессе заполнения изменяется незначительно, тогда как температура поверхности формы резко возрастает.
После рассмотрения критерия Bi как отношения температурного перепада δt к температурному напору Δt можно заключить, что в процессе заполнения температурный напор очень мал по сравнению с температурным перепадом Bi>>1 (процесс характеризуется большой относительной интенсивностью теплообмена).
При определении потерь тепла через поверхность соприкосновения расплава и формы параметрический критерий х/Х = 1. Вэтом случае критериальное уравнение (77) имеет вид
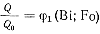
где Q0 = Vфρфсфϑф — количество теплоты, которое может аккумулировать форма при охлаждении отливки от температуры начала заполнения t0 до температуры tс, т. е. при начальном температурном напоре ϑф = tф — tс.
Для определения зависимости коэффициента теплоотдачи от времени А. И. Вейник предлагает воспользоваться простой степенной зависимостью
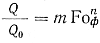
откуда
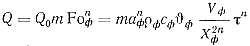
(так как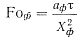 
) или в
дифференциальной форме
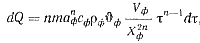
где m — коэффициент, зависящий от конфигурации отливки и формы; n — показатель степени, который в зависимости от интенсивности теплообмена может изменяться от ½ до 1. В условиях максимальной интенсивности n=½. Коэффициент теплоотдачи на поверхности отливки и формы определяется отношением
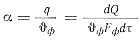
После подстановки значения dQ из выражения (78) и некоторых преобразований получим
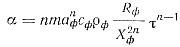(79)
где Rф=Vф/Fф — приведенный размер формы.
Поскольку любые тонкостенные отливки можно рассматривать как плоские, то значение коэффициента m из общей теории теплопроводности определяется следующей формулой:
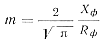
Подставляя значение m в выражение (79), найдем уравнение для определения коэффициента теплоотдачи при различной интенсивности теплообмена:
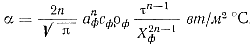(80)
Для алюминиевых сплавов, заливаемых сплошным потоком, с высокоразвитой турбулентностью при отсутствии смазки можно принять условие максимальной интенсивности теплообмена, т. е. n = ½. В этом случае уравнение (80) имеет наиболее простое выражение:
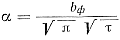(81)
где bф = √λфсфρф — коэффнциент тепловой аккумуляции формы в вт·сек ½ /м2°С.
