Дифференциальные уравнения движения охлаждающегося потока металла
Во время заполнения литниковых каналов и полости формы расплавленный металл интенсивно охлаждается.
По мере охлаждения вязкость металла повышается и этим изменением вязкости нельзя пренебрегать при определении закона распределения скоростей и давления в потоке. Соответственно процесс движения расплавленного металла в отличие от уравнений Навье-Стокса (3) выражается системой дифференциальных уравнений, в которых вязкость является переменной функцией, зависящей от температуры v = φ(t) и координат v = φ1(x, y, z):
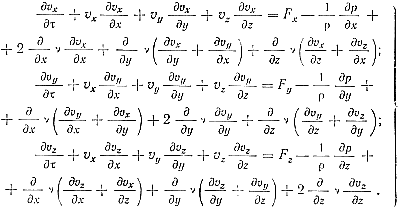 (13)
(13)
Так как здесь v = q(t), то данная система из трех уравнений содержит пять неизвестных функций: υx, υy, υz, p и t. Чтобы система стала полной, присоединим к ней еще два уравнения — неразрывности и притока тепла:
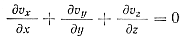 (14)
(14)
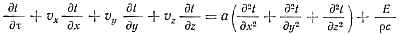 (15)
(15)
где а — коэффициент температуропроводимости, а =λ/cρ в м2/сек; E—функция рассеивания, определяющая переход механической энергии в тепловую при движении вязкой жидкости,
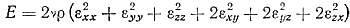
здесь εii — компоненты скоростей деформации жидкости
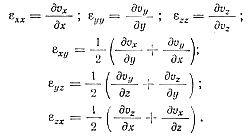
Для решения частной задачи движения расплавленного металла в форме при небольших скоростях впуска и плоскопараллельном режиме заполнения систему уравнений можно значительно упростить.
 |
Рассмотрим установившееся течение вязкого металла, происходящее параллельно оси х, между неподвижными плоскостями у =H/2 и y= -H/2 (рис. 37). Обозначив ширину отливки через В, принимаем условие, что H/B<<1, позволяющее считать отливку плоским каналом. Рис. 37. Движение металла в плоском канале |
В условиях допущения ламинарного движения υy = 0, υz = 0, υx = υ, уравнение неразрывности (14) имеет вид дυ/дх=0
Левые части уравнений (13) представляют собой проекции на оси координат ускорений движущихся частиц металла и, следовательно, для установившегося движения равны нулю.
Действием массовых сил пренебрегаем Fx = Fy = Fz = 0.
В уравнении притока тепла (15) при установившемся движении дυ/дх=0, дt/дz=0 так как рассматривается теплоотдача через плоскую стенку.
Подставляя все эти допущения в уравнения (13), (14), (15), после некоторых преобразований получим новую систему дифференциальных уравнений движения расплавленного металла в форме:
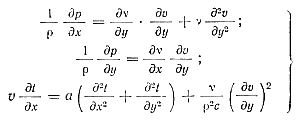 (16)
(16)
где
v=φ(t)