Распределение скоростей и изменение давления в процессе заполнения сплошным потоком

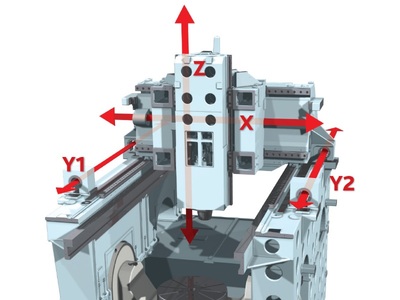
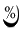Для определения законов распределения скоростей и изменения давления в процессе заполнения сплошным потоком необходимо решить систему уравнений (16).

Так как аналитически решить данные уравнения невозможно, то рассмотрим задачу в более простой постановке, данной академиком Л. С. Лейбейзоном для случая движения подогретой вязкой жидкости в круглой трубе, применив ее для движения расплавленного металла в плоском канале.

Допустим, что температура металла постоянна в каждом сечении и изменяется только вдоль оси x. Обозначим среднюю температуру сечения через t_cp.

В этом случае t_cp = φ(х), а следовательно, и v = φ(x), так как v = φ(t).

Продифференцируем обе части первого уравнения системы (16) по ду, а второго уравнения до дх, после преобразований получим

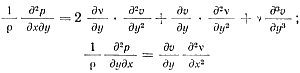
После вычитания из первого выражении второго исключим давление p и получим новое дифференциальное уравнение третьего порядка:

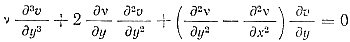              (17)

Так как вязкость изменяется только вдоль оси х, то дv/дy=0 и уравнение (17) принимает вид

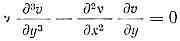
Разделив переменные и приравнивая обе части уравнения какой-то постоянной величине, которую для удобства дальнейшего решения представим в виде (2m)²/H² (где m — безразмерная величина, а H — толщина отливки), можем записать

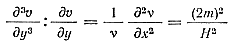                            (18)

Для определения зависимости v от x выделим из уравнения (18) правую часть

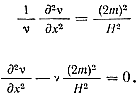
или

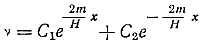
Отсюда после интегрирования получим

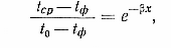                                           (19)

Определим закон изменения температуры вдоль оси x и перейдем от зависимости v = φ(х), выраженной уравнением (19), к зависимости v = φ(t).

Количество тепла, отдаваемое элементом потока расплавленного металла через стенки формы за время dτ,

d²Q = α(t_cp-t_ф)dFdτ,

где α — коэффициент теплоотдачи; t_ф — температура стенок формы; dF— поверхность теплоотдачи, dF = 2(H + B)dx.

За это же время приток тепла вследствие конвективного переноса в данный объем металла составит

d²Q₁= -cρdt_cpHBυ_cpdτ.

Если пренебречь рассеянием энергии, то

d2Q = d2Q₁,
α (t_cp - t_ф) 2 (H + В) dxdτ = - cρdt_cp HBυ_cpdτ,

откуда после разделения переменных, интегрирования и подстановки граничных условий (при x = 0, t_cp = t₀) получим для капала прямоугольного сечения

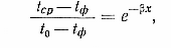                                 (20)

где

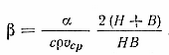
Здесь υ_cp — средняя по сечению скорость потока, определяемая по уравнению неразрывности для системы «камера прессования — отливка».

После введения в уравнение (20) вместо x новой переменной x1=x/H и замены отношения температур безразмерной величиной 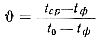 можем записать

ϑ=e^-βx1

Отсюда

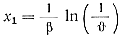
После замены в уравнении (19) постоянных С₁ и С₂ новыми v₀ и С и подстановки вместо x/H=x₁ получим его выражение через безразмерную величину ϑ:

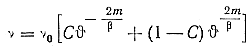                    (21)

где v₀ — кинематическая вязкость при t = t₀.

Для дальнейшего расчета необходимо воспользоваться экспериментальными зависимостями v =φ(t), по которым можно построить графические закономерности v / v φ (ϑ) для определения постоянных величин m и С.

Закон изменения скорости по сечению потока υ = φ(y) находим из дифференциального уравнения (18), которое можно представить в виде

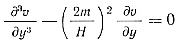                          (22)

Решение уравнения (22) записывается выражением

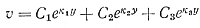
корни которого определяются из характеристического уравнения

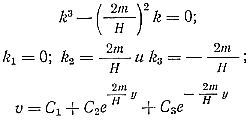
Определяем постоянные интегрирования из условий, что при у = 0, υ = υ_max и при у = ± Н/2 , υ = 0,

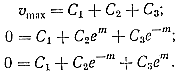
Решая данную систему уравнений, находим

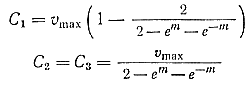
Подставляя значения С₁, С₂ и С₃ и сделав некоторые преобразования, получим

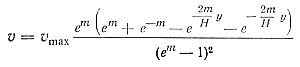                       (23)

υ_cp, которая определяется по расходу жидкого металла:

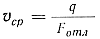
Секундный расход для прямоугольного сечения

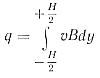
или после подстановки v из выражения (23) и интегрирования

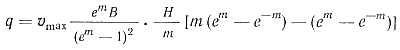
Разделив обе части данного выражения   на площадь отливки F_отл = НВ получим

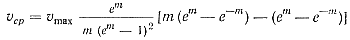
После выделения отсюда υ_max и подстановки его в выражение (23) находим окончательный закон распределения скоростей в потоке металла с переменной вязкостью

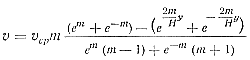
Определим закон изменения давления по потоку. Из первого уравнения системы (16) при условии изменения вязкости только вдоль оси x имеем

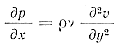
Подставив значение υ из закона распределения скоростей (24) и продифференцировав, получим

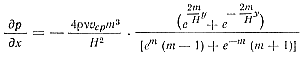                   (25)

Заменим давление p средним по сечению p_cp, которое будет изменяться только вдоль оси x:

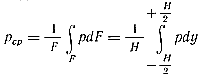
После умножения обеих частей равенства (25) на dy/H и интегрирования по у от -H/2 до + H/2 , имеем

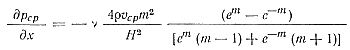
Подставим значение v из ранее полученного уравнения (21) с заменой ϑ=e^-βx1, где х₁=x/H. Затем проинтегрируем по x, полагая, что при x = 0 р_cp = p₀, а при x = 1 (1 — длина участка падения давления) р_cp = p₁, получим

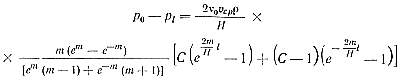                     (26)

Разность p₀ — p₁ в формуле (26) означает падение давления при прохождении потоком пути l со средней скоростью υ_cp.