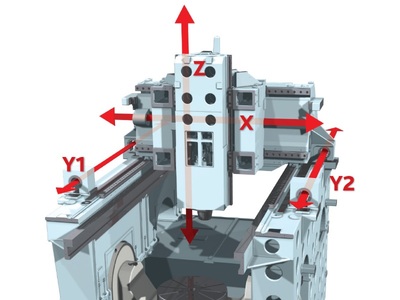
Температура расплава в начале заполнения формы tзал отличается от температуры металла в раздаточной печи tp.n на величину потерь в разливочном ковше Δtк, камере прессования машины Δtпр и в литниковой системе Δtл:
tзал = tр.п - Δtк — Δtрп-Δtл.
Для расчета охлаждения металла в разливочном ковше можно воспользоваться формулой, предложенной А. И. Вейником:
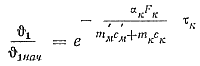 (82)
(82)
где ϑ1 — температура сплава в ковше, отсчитываемая от tс, как от нуля, в °С;
ϑ1 = tк – tс,
ϑнач — начальная избыточная температура сплава в раздаточной печи в °С,
ϑ1нач = tр.п – tс,
αк — коэффициент теплообмена на поверхности контакта сплава и ковша, по расчетам А. И. Вейника равный для алюминиевых сплавов 67,7 вт1м2°С (0,0162 ккал/м2 сек °С), а для цинковых — 34,8 вт/м2 °С (0,0083 ккал/м2сек°С); Fк — площадь поверхности контакта сплава с ковшом в м2; m'м— масса порции сплава в ковше в кг; mк — масса раздаточного ковша в кг; с'м—удельная теплоемкость жидкого металла в дж/кг°С; ск — удельная теплоемкость материала ковша в дж/кг°С; τк — время нахождения сплава в ковше в сек.
В дальнейшем для упрощения расчетной формулы воспользуемся приближенной заменой экспоненциальной функции двумя первыми членами степенного ряда, считая такую замену возможной для малых отрезков времени. В этом случае, подставляя значения ϑ1 и ϑ1 нач в формулу (80), получим
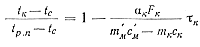
откуда, после преобразований, определим температуру сплава в ковше в момент времени τк:
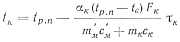 (83)
(83)
Определим конкретные зависимости температуры от времени нахождения алюминиевых и цинковых сплавов в ковше, принимая массу ковша mк = 1 кг ((ск = 670 дж/кг°С) [0,16 ккал/кГ°С] для чугуна), объем порции жидкого металла 125-10-6 м3, поверхность теплоотдачи Fк = 0,015 м2, температуру окружающей среды tс = 20°С.
Для алюминиевых сплавов масса порции жидкого металла равна m'м = 125·10-6· 2500 = 0,313 кг. Подставляя значения величин в формулу (83) при tр.п = 650°С и с'м = 1290 дж/кг°С (0,308 ккал/кГ °С), найдем

Соответственно для цинковых сплавов при mк= 125x10-6·6700 = 0,838 кг, tр.п = 450° С и с'м = 531 дж/кг °С (0,127ккал/кГ°С) получим
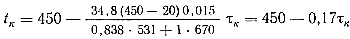
Данные зависимости выведены при условии предварительного подогрева разливочного ковша до температуры металла. В этом случае понижение температуры будет минимальным. Например для алюминиевых сплавов оно составляет 5,9° за 10 сек, а для цинковых — 1,7°.
Расчетная формула для охлаждения сплава в камере прессования имеет вид
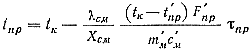 (84)
(84)
где tпр — температура сплава в камере прессования в момент времени τnр; λсм — коэффициент теплопроводности смазки в вт/м°С; Хсм — толщина слоя смазки в м; t'пр — температура предварительного подогрева камеры прессования в °С; F'пр — площадь поверхности теплоотдачи в м2.
В формуле (84) отношение λсм/Хсм играет роль соответствующего коэффициента теплоотдачи от жидкого металла к поверхности камеры прессования.
Скорость охлаждения металла в камере прессования значительно превышает скорость охлаждения в разливочном ковше. Определим зависимости падения температуры Δtпр = tк — tпр от времени нахождения металла в камере прессования τпр для алюминиевых и цинковых сплавов при различной толщине слоя смазки Хсм, если коэффициент теплопроводности смазки λсм = 0,12 вт/м°С (28·10-6 ккал/мсек°С).
В расчетах используем числовые значения из предыдущей задачи определения температурных потерь в разливочном ковше.
Для алюминиевых сплавов при температуре подогрева камеры прессования t'пр = 250° находим
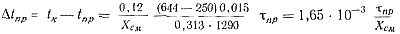
где Хсм в м.
Для цинковых сплавов при t'пр = 150°

Данные зависимости, представленные графически на рис. 88, a и б, показывают, что падение температуры в камере прессования обратно пропорционально толщине слоя смазки.
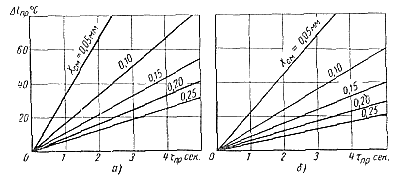 |
Рис. 88. Зависимость изменения температуры в камере прессования от времени при различной толщине слоя смазки для алюминиевых (а) и цинковых (б) сплавов |
Время отвода всей теплоты перегрева для алюминиевого сплава АЛ2 (∆tпр = 644 — 590 = 54°) при толщине слоя смазки Хсм = 0,1 мм = 0,1·10-3 м составит
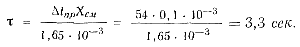
Для цинкового сплава ЦЛМ4-3 (Δtпр = 448 — 390 = 58°)
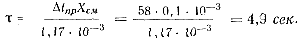
Для предотвращения преждевременного отвода теплоты перегрева от расплава необходимо увеличивать толщину слоя смазки, температуру подогрева камеры t'пр и главное — сокращать время нахождения жидкого металла в камере прессования машины.
Потерями тепла в литниковой системе при работе на машинах с горизонтальной камерой прессования можно пренебречь, так как длина литниковой системы очень мала.
Для машин с вертикальной камерой прессования определим потери тепла при прохождении металла в коническом литнике. При этом предположим, что диаметр литника постоянный, равный среднему диаметру конического канала, размер которого зависит от тина машины.
Рассмотрим тепловые условия для элементарного объема жидкого металла в форме цилиндра с радиусом Rл и высотой dL.
Приток тепла dQ вследствие конвекции в единицу времени равен
dQ = -πR2лс'мρ'мυлdt
За это время из данного объема через стенки литникового канала уйдет следующее количество тепла:
dQ1 = αл(tл-t'л)2πRлdL.
Если пренебречь изменением температуры при рассеянии энергии, то указанные выше количества тепла должны быть равны
Rлс'мρ'мυлdt= — 2αл(tл — t'л) dL.
Интегрируя это равенство и удовлетворяя его граничному условию tл = tпр при L = 0, получим уравнение для определения температуры жидкого металла tл при выходе из литника:
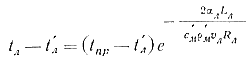 (85)
(85)
где t'л —температура стенок литника, равная температуре прессформы tф; tпр — температура металла, поступающего из камеры прессования в литниковую систему, определяется по формуле (84); Lл и Rл —длина и радиус литника.
Для подсчета коэффициента теплоотдачи αл воспользуемся выводами Г. Ф. Баландина, по которым для течения металла в литниковых каналах можно сделать допущение по аналогии с литьём выжиманием — вначале охлаждаются только пристеночные слои жидкости, а температура центра потока остается постоянной. В этом случае коэффициент теплоотдачи в литниковом канале
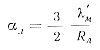
где λ'м — коэффициент теплопроводности жидкого металла в вт/м °С.
Скорость течения металла в литнике определяется уравнением неразрывности потока для системы «камера прессования — литниковый канал»
υлFл = υпрFпр
откуда
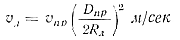
После замены экспоненты в уравнении (85) двумя первыми членами степенного ряда и преобразований получим приближенную расчетную формулу для определения температуры жидкого металла tл после прохождения литникового канала длиной Lл:
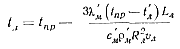 (86)
(86)
В формуле (86) отношение Lл/υл соответствует времени протекания металла через литниковый канал.
Например, при длине литника Lл = 150 мм, Rл = 10 мм и скорости течения υл = 10 м/сек для алюминиевых сплавов [tпр = 620°, t'л = 250° и λ'м= 352 вт/м°С (0,084 ккал/м сек°С)] найдем
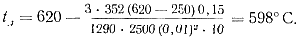
Соответственно для цинковых сплавов [tпр = 420°, t'л = 150° и λ'м = 101 вт/м°С (0,024 ккал/мсек°С)] имеем
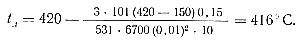
Следует учесть, что формула (86) выведена при условии отсутствия смазки. Наличие теплоизолирующей смазки на поверхности литникового канала в некоторой степени снижает потери тепла.
Если пренебречь разогревом металла в питателе, то температура расплава на выходе из литника tл будет равна начальной температуре заливки в полость формы tзал.