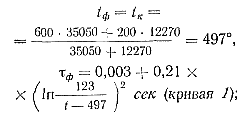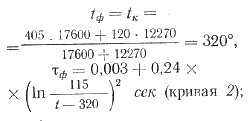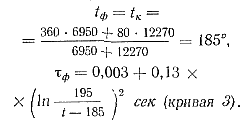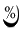Время заполнения полости формы

Время заполнения полости формы определяется из рассмотрения процесса теплообмена между заливаемым металлом и формой.

Время заполнения, обеспечивающее свариваемость отдельных струй или брызг, подсчитывается из условия, что температура металла в наиболее удаленном от питателя месте не должна падать ниже температуры окончания затвердевания (ниже температуры солидуса).

Для определения потерь тепла в полости формы в процессе ее заполнения предположим, что сплошной турбулентный поток заполняет форму от дальнего сечения к питателю. Тогда скорость продвижения потока металла в полости формы

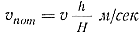
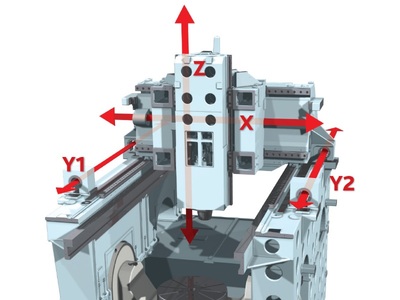
где h — толщина струи; H — толщина  отливки при условии, что ширина питателя равна ширине отливки (рис. 89).

Выделим из потока элементарный объем жидкости и рассмотрим его тепловое состояние. За какой-то бесконечно малый промежуток времени данный объем, соприкасаясь со стенками формы, отдает следующее количество тепла:

d²Q = α_ф(t-t_ф)dFdτ,                      (87)

где dF — площадь теплоотдачи, равная 2dxdz.

Рис. 89. Схема выделения элементарного объема в потоке для рассмотрения процесса теплопередачи За то же время dτ теплосодержание выделенного элементарного объема dV=Hdxdz уменьшится на величину d2Q = — Hdx dzc'мρ'мdt.                       (88)

Приравняв выражения (87) и (88) получим дифференциальное уравнение теплового баланса в общем виде:

2α_ф(t-t_ф)dτ = -Hc'_мρ'_мdt,                               (89)

решение которого зависит от вида функций α_ф = φ(τ)

При условиях сплошного турбулентного заполнения, максимальной интенсивности теплообмена и пренебрежения влиянием смазки коэффициент теплоотдачи определяется выражением (81):

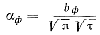
В этом случае после разделения переменных уравнение (89) имеет вид

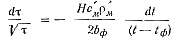
Найдя постоянную интегрирования из условия, что в начале заполнения при τ = 0, t = t_зал получим

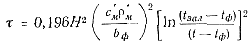                         (90)

Максимально допустимое время заполнения τ_max находится при температуре потока t, равной температуре солидуса t_сол.

Формула (90) не учитывает времени свободного полета и растекания струи до момента возникновения сплошного потока по всему сечению.

Приближенно это время

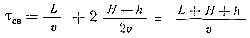
Общее время заполнения полости формы

τ_ф ≤ τ_св + τ_max

или после  подстановки  значения τmax из формулы (90) при t=t_сол

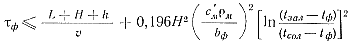                                    (91)

Формулу (90) можно упростить, подставив значения коэффициента тепловой аккумуляции для стальной формы b_ф == 12 270 вт·сек ^½м2°С (2,96 ккал/м2сек^½ °С) и теплофизических характеристик для различных сплавов:

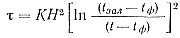                                       (92)

где К — постоянная величина, равная для медных сплавов 0,025, магниевых 0,005, алюминиевых 0,013, цинковых 0,015 и для свинцово-сурьмянистых 0,008; H — средняя толщина отливки в мм.

Для определения средней толщины стенки отливок сложной конфигурации вводится понятие эквивалентной отливки, у которой толщина стенки

Н_экв=2М_отл,

где M_отл — приведенный размер или «модуль» отливки;

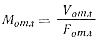
где F_отл — площадь поверхности охлаждения отливки.

Для неограниченной плоской стенки и приближенно для тонкостенных отливок любой конфигурации М_отл = Н, для бесконечно длинного круглого цилиндра M = R/2 и для шара M =R/3.

В формулах (90), (91) и (92) под t_ф подразумевается температура поверхностных слоев формы, т. е. температура контакта, определяемая формулой (68):

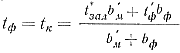
где t*_зал — средняя температура заливки за время заполнения,

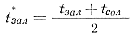
t'_ф —температура предварительного подогрева формы.

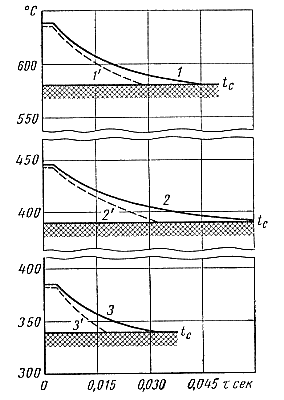
На рис. 90 представлены графические зависимости температуры от времени с учетом времени свободного полета при заполнении прямоугольной отливки длиной 85 мм, толщиной 4 мм (кривые 1, 2 и 3) и 3 мм (кривые 1', 2' и 3) при скорости впуска υ = 30 м/сек.]

Формулу (92) в условиях заливки различными сплавами можно представить в цифровом виде: а) для алюминиевого сплава АЛ2 при t'ф = 200 °С и б) для цинкового сплава ЦАМ 4-3 при t'ф = 120° и   в) для свинцово-сурьмянистого сплава (80% Pb, 20% Sb) при t'ф = 80° и Рис. 90. Изменение температуры в зависимости от времени заполнения для различных сплавов

На рис. 90 пунктиром обозначены аналогичные зависимости при толщине отливки 3 мм.

При заполнении формы дисперсным потоком интенсивность теплообмена снижается вследствие образования смеси капель металла с воздухом. Исследования температурных условий формирования отливок при заполнении дисперсным потоком доказали, что показатель интенсивности теплообмена n в критериальном уравнении (80) близок к ⅔.

Решая уравнение (80) при n = ⅔, получим

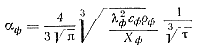
или

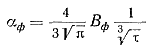                    (93)

где 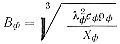  — коэффициент тепловой аккумуляции формы в условиях дисперсного заполнения. Для стальной формы при Х_ф равном в среднем 50 мм, В_ф = 4485 вт·сек^⅓/м2°С (1,07 ккал/м2 сек^⅔°С).

Подставляя значение α_ф из выражения (93) в уравнение теплового баланса, после разделения переменных имеем

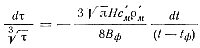
откуда после интегрирования при граничных условиях τ = 0, t = t_зал получим формулу для определения времени заполнения:

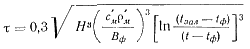
или в более простом виде

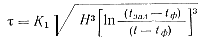                        (94)

где Н — средняя толщина стенки отливки в мм; К₁ — постоянная величина, равная для медных сплавов 0,236, магниевых 0,100, алюминиевых 0,179, цинковых — 0,201 и для свинцово-сурьмянистых сплавов 0,101.

В табл. 6 приведены значения времени дисперсного заполнения при различной толщине стенок, подсчитанные по формуле (94) при t = t_сол.

Таблица 6. Значения времени дисперсного заполнения в сек

Температура поверхности формы в условиях дисперсного потока достигает температуры контакта только после окончания заполнения. Поэтому рекомендуется при расчетах по формуле (94) использовать следующие значения tф для сплавов: медных 450° С, магниевых 350° С: алюминиевых 350° С, цинковых 200° С, свинцово-сурьмянистых 150°С.

Анализ формул (92) и (94) показывает, что при создании определенных тепловых условий время заполнения зависит главным образом от толщины стенки отливки и не зависит от ее габаритов.

В то же время на практике можно часто встретиться с необоснованным увеличением времени заполнения для крупных отливок, которое снижает качество изделий.

Расчеты по формуле (94) близки к графическим зависимостям, полученным Ф. Беннеттом для магниевых, алюминиевых и цинковых сплавов (рис. 91).

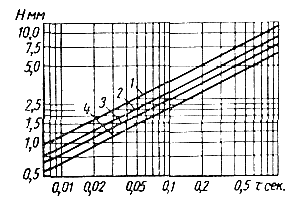Рис. 91. Зависимость времени заполнения т от средней толщины Н стенки отливок для чистого магния (1), для магниевых (2), алюминиевых (3) и цинковых (4) сплавов